如图所示,已知圆 为圆上一动点,点
为圆上一动点,点 是线段
是线段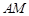 的垂直平分线与直线
的垂直平分线与直线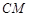 的交点.
的交点.
(1)求点 的轨迹曲线
的轨迹曲线 的方程;
的方程;
(2)设点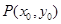 是曲线
是曲线 上任意一点,写出曲线
上任意一点,写出曲线 在点
在点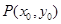 处的切线
处的切线 的方程;(不要求证明)
的方程;(不要求证明)
(3)直线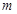 过切点
过切点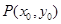 与直线
与直线 垂直,点
垂直,点 关于直线
关于直线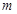 的对称点为
的对称点为 ,证明:直线
,证明:直线 恒过一定点,并求定点的坐标.
恒过一定点,并求定点的坐标.
推荐套卷
如图所示,已知圆 为圆上一动点,点
为圆上一动点,点 是线段
是线段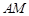 的垂直平分线与直线
的垂直平分线与直线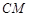 的交点.
的交点.
(1)求点 的轨迹曲线
的轨迹曲线 的方程;
的方程;
(2)设点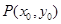 是曲线
是曲线 上任意一点,写出曲线
上任意一点,写出曲线 在点
在点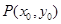 处的切线
处的切线 的方程;(不要求证明)
的方程;(不要求证明)
(3)直线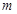 过切点
过切点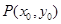 与直线
与直线 垂直,点
垂直,点 关于直线
关于直线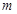 的对称点为
的对称点为 ,证明:直线
,证明:直线 恒过一定点,并求定点的坐标.
恒过一定点,并求定点的坐标.