如图，⊙O的直径AB=6cm，P是AB延长线上的一点，过点P作⊙O的切线，切点为C，连接AC，BC．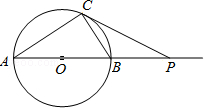
（1）若∠CPA=30°，求PC的长；
（2）探究：当点P在AB的延长线上运动时，是否总存在∠PCB=∠CAB？若存在，请证明；若不存在，请说明理由．
相关试题
已知二次函数
的图象如图所示，它与x轴的一个交点坐标为（－1，0），与y轴的交点坐标为（0，3）。
（1）求出b，c的值，并写出此二次函数的解析式；
（2）根据图象，写出函数值y为正数时，自变量x的取值范围
如图，在平面直角坐标系中，四边形ABCD的四个顶点的坐标分别是A（1，3）、
B（2，2）、C（2，1），D（3，3）．
（1）以原点O为位似中心，相似比为2，将图形放大，画出符合要求的位似四边形；
（2）在（1）的前提下，写出点A的对应点坐标A′
如图10-1，在平面直角坐标系
中，点
在
轴的正半轴上， ⊙交轴于 
两点，交
轴于
两点，且
为
的中点，
交轴于
点，若点
的坐标为（－2，0），
(1)(3分)求点的坐标.
(2)(3分)连结
，求证：
∥
(3)(４分) 如图10-2，过点
作⊙的切线，交轴于点
.动点
在⊙的圆周上运动时，
的比值是否发生变化，若不变，求出比值；若变化，说明变化规律
如图9，抛物线
与
轴交于
、
两点（点在点的左侧），抛物线上另有一点
在第一象限，满足∠
为直角,且恰使△
∽△
.
(1)(3分)求线段
的长.
(2)(3分)求该抛物线的函数关系式．
(3)(4分)在轴上是否存在点
，使△
为等腰三角形？若存在，求出所有符合条件的点的坐标；若不存在，请说明理由.
推荐套卷
粤公网安备 44130202000953号