已知函数 ,
,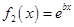 .
.
(1)若 ,是否存在
,是否存在 、
、 ,使
,使 为偶函数,如果存在,请举例并证明你的结论,如果不存在,请说明理由;
为偶函数,如果存在,请举例并证明你的结论,如果不存在,请说明理由;
(2)若 ,
, ,求
,求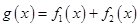 在
在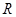 上的单调区间;
上的单调区间;
(3)已知 ,
,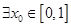 对
对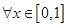 ,,有
,,有 成立,求
成立,求 的取值范围.
的取值范围.
相关知识点
推荐套卷
已知函数 ,
,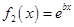 .
.
(1)若 ,是否存在
,是否存在 、
、 ,使
,使 为偶函数,如果存在,请举例并证明你的结论,如果不存在,请说明理由;
为偶函数,如果存在,请举例并证明你的结论,如果不存在,请说明理由;
(2)若 ,
, ,求
,求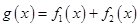 在
在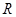 上的单调区间;
上的单调区间;
(3)已知 ,
,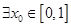 对
对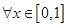 ,,有
,,有 成立,求
成立,求 的取值范围.
的取值范围.