已知A、B两市相距200千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障不能行驶,立即通知技术人员乘乙车从A市赶去维修(通知时间忽略不计),乙车到达M地后用24分钟修好甲车后以原速度原路返回,同时甲车以原速1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车的行驶时间x(小时)之间的函数图象,结合图象回答下列问题:
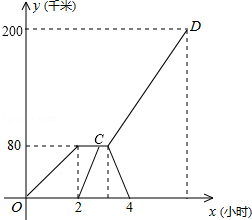
(1)甲车提速后的速度是 千米/小时,点C的坐标是 ,
(2)求乙车返回时y与x之间的函数关系式并写出自变量x的取值范围;
(3)乙车返回A市多长时间后甲车到达B市.