如图，在直角坐标系中，点A的坐标为(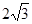
，0)，连结OA，将线段OA绕原点O顺时针旋转120°，得到线段OB．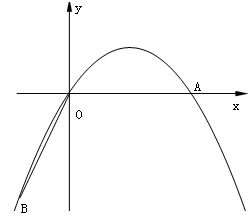
（1）请直接写出点B的坐标；
（2）求经过A、O、B三点的抛物线的解析式；
（3）如果点P是（2）中的抛物线上的动点，且在x轴的上方，那么△PAB是否有最大面积？若有，求出此时P点的坐标及△PAB的最大面积；若没有，请说明理由．
相关试题
中，点
是
的中点，且
⊥
．
的度数；
的长；
为一梯形纸片，
∥
，
．翻折纸片
与点
重合，折痕为
．已知
⊥
.
中，
∥
，
，
⊥
，延长
至点
，使
．
的度数．
为等腰三角形．
中，
是
边上一点，
的延长线交
的延长线于点
，
⊥
，垂足为
，且
．
；
相关知识点
推荐套卷
如图，在直角坐标系中，点A的坐标为(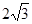，0)，连结OA，将线段OA绕原点O顺时针旋转120°，得到线段OB．
（1）请直接写出点B的坐标；
（2）求经过A、O、B三点的抛物线的解析式；
（3）如果点P是（2）中的抛物线上的动点，且在x轴的上方，那么△PAB是否有最大面积？若有，求出此时P点的坐标及△PAB的最大面积；若没有，请说明理由．
粤公网安备 44130202000953号