若对任意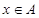 ,
,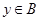 ,(
,(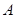 、
、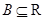 )有唯一确定的
)有唯一确定的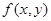 与之对应,称
与之对应,称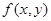 为关于
为关于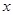 、
、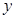 的二元函数.现定义满足下列性质的二元函数
的二元函数.现定义满足下列性质的二元函数 为关于实数
为关于实数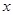 、
、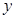 的广义“距离”:
的广义“距离”:
(1)非负性: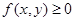 ,当且仅当
,当且仅当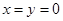 时取等号;
时取等号;
(2)对称性: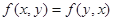 ;
;
(3)三角形不等式: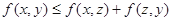 对任意的实数z均成立.
对任意的实数z均成立.
今给出四个二元函数:
①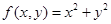 ;②
;②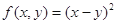 ③
③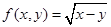 ;④
;④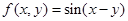 .
.
能够成为关于的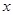 、
、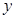 的广义“距离”的函数的所有序号是 .
的广义“距离”的函数的所有序号是 .
相关知识点
推荐套卷
若对任意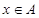 ,
,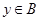 ,(
,(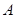 、
、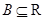 )有唯一确定的
)有唯一确定的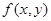 与之对应,称
与之对应,称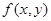 为关于
为关于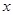 、
、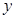 的二元函数.现定义满足下列性质的二元函数
的二元函数.现定义满足下列性质的二元函数 为关于实数
为关于实数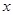 、
、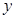 的广义“距离”:
的广义“距离”:
(1)非负性: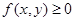 ,当且仅当
,当且仅当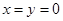 时取等号;
时取等号;
(2)对称性: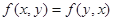 ;
;
(3)三角形不等式: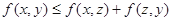 对任意的实数z均成立.
对任意的实数z均成立.
今给出四个二元函数:
①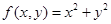 ;②
;②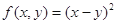 ③
③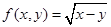 ;④
;④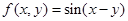 .
.
能够成为关于的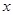 、
、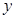 的广义“距离”的函数的所有序号是 .
的广义“距离”的函数的所有序号是 .