如图，AC是圆O的直径，点B在圆O上，
，
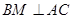交AC于点M，EA⊥平面ABC，FC∥EA，AC=4，EA=3，FC=1,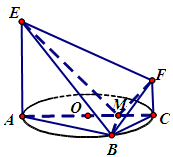
（1）证明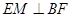
；
（2）（文科）求三棱锥
的体积
（理科）求平面
和平面
所成的锐二面角的正切值.
相关试题
的上顶点为
,右焦点为
,直线
与圆
相切.
的方程；
与椭圆
、
两点，且
求证：直线
的坐标.
中，
，
，
．
是等比数列；
项和
，求
的最大值
，在函数
的图象中，对称中心到对称轴的最小距离为
且当
的最大值为1。
的解析式；
的不等式
相关知识点
推荐套卷
如图，AC是圆O的直径，点B在圆O上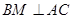，，交AC于点M，EA⊥平面ABC，FC∥EA，AC=4，EA=3，FC=1,
（1）证明；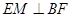
（2）（文科）求三棱锥的体积
（理科）求平面和平面所成的锐二面角的正切值.
粤公网安备 44130202000953号