现有甲、乙两个靶.某射手向甲靶射击两次,每次命中的概率为
,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为
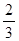,命中得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
(I)求该射手恰好命中两次的概率;
(II)求该射手的总得分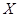
的分布列及数学期望
;
相关试题
，函数
，
的单调区间；
，不等式
恒成立，求
的取值范围。
，
，且
，求实数
的取值范围。
（
）
满足什么条件时，z是实数？
（2）
（4）
中，
⊥面
，
，
，
为
的中点.
；
的余弦值；
，使得
？请证明你的结论.
推荐套卷
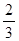现有甲、乙两个靶.某射手向甲靶射击两次,每次命中的概率为,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为,命中得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
(I)求该射手恰好命中两次的概率;
(II)求该射手的总得分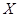的分布列及数学期望;
粤公网安备 44130202000953号