如图，为了测量山顶铁塔AE的高，小明在27m高的楼CD底部D测得塔顶A的仰角为45°，在楼顶C测得塔顶A的仰角36°52′．已知山高BE为56m，楼的底部D与山脚在同一水平线上，求该铁塔的高AE．（参考数据：sin36°52′≈0.60，tan36°52′≈0.75）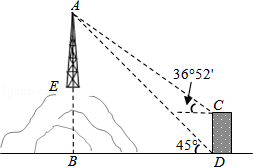
=1，求（x+1）（x﹣1）+（2x﹣1）2的值．相关知识点
推荐套卷
如图，为了测量山顶铁塔AE的高，小明在27m高的楼CD底部D测得塔顶A的仰角为45°，在楼顶C测得塔顶A的仰角36°52′．已知山高BE为56m，楼的底部D与山脚在同一水平线上，求该铁塔的高AE．（参考数据：sin36°52′≈0.60，tan36°52′≈0.75）
粤公网安备 44130202000953号