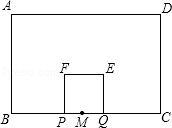
如图,在矩形ABCD中,AD=8,AB=6,点M是BC的中点,点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动,在点P,Q的运动过程中,以PQ为边作正方形PQEF,使它与矩形ABCD在BC的同侧,点P,Q同时出发,当点P返回点M时停止运动,点Q也随之停止,设点P,Q运动的时间是t秒(t>0)
(1)用含t的代数式表示线段BQ的长;
(2)设正方形PQEF与矩形ABCD重叠部分的面积为S,求S与t之间的函数关系式;
(3)连接AC,当正方形PQEF与△ADC重叠部分为三角形时,直接写出t的取值范围.