如图，在直角坐标系中，点A的坐标为（﹣2，0），点B的坐标为（1，
），已知抛物线y=ax2+bx+c（a≠0）经过三点A、B、O（O为原点）．
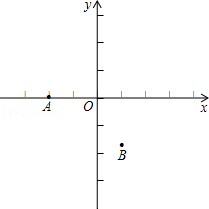
（1）求抛物线的解析式；
（2）在该抛物线的对称轴上，是否存在点C，使△BOC的周长最小？若存在，求出点C的坐标；若不存在，请说明理由；
（3）如果点P是该抛物线上x轴上方的一个动点，那么△PAB是否有最大面积？若有，求出此时P点的坐标及△PAB的最大面积；若没有，请说明理由．（注意：本题中的结果均保留根号）
相关试题
一共要70元,买 
一共要50元.已知：如图BE//CF，BE、CF分别平分∠ABC和∠BCD, 求证：AB//CD
证明：∵ BE、CF分别平分∠ABC和∠BCD（已知）
∴ ∠1=
∠∠2=∠（ ）
∵ BE//CF（）
∴ ∠1=∠2（）
∴ ∠ABC=∠BCD
即∠ABC=∠BCD
∴ AB//CD（）
为了了解学生的身体素质，某校体育教师对初中学生进行引体向上测试，将所得的数据进行整理，画出统计图，图中从左到右依次为第1、2、3、4、5组。
（1）求抽取了多少名学生参加测试；
（2）处于哪个次数段的学生人数最多；
（3）若次数在5次（含5次）以上为达标，求这次达标率。
相关知识点
推荐套卷
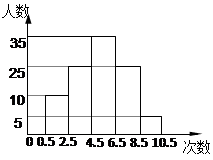
粤公网安备 44130202000953号