如图，平面直角坐标系中，直线l分别交x轴、y轴于A、B两点（OA＜OB）且OA、OB的长分别是一元二次方程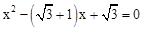
的两个根，点C在x轴负半轴上，
且AB：AC=1：2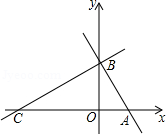
（1）求A、C两点的坐标；
（2）若点M从C点出发，以每秒1个单位的速度沿射线CB运动，连接AM，设△ABM的面积为S，点M的运动时间为t，写出S关于t的函数关系式，并写出自变量的取值范围；
（3）点P是y轴上的点，在坐标平面内是否存在点Q，使以 A、B、P、Q为顶点的四边形是菱形？若存在，请直接写出Q点的坐标；若不存在，请说明理由．
相关试题
在足球比赛场上,甲、乙两名队员互相配合向对方球门MN进攻.当甲带球部到A点时,乙随后冲到B点,如图所示,此时甲是自己直接射门好,还是迅速将球回传给乙,让乙射门好呢?为什么?(不考虑其他因素)
如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.
(1)P是
上一点(不与C、D重合),试判断∠CPD与∠COB的大小关系, 并说明理由.
(2)点P′在劣弧CD上(不与C、D重合时),∠CP′D与∠COB有什么数量关系?请证明你的结论.
相关知识点
推荐套卷
粤公网安备 44130202000953号