对于三次函数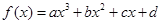
 ,给出定义:设
,给出定义:设 是函数
是函数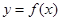 的导数,
的导数,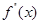 是函数
是函数 的导数,若方程
的导数,若方程 有实数解
有实数解 ,则称点
,则称点 为函数
为函数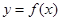 的“拐点”。某同学经过探究发现:任何一个一元三次函数都有“拐点”;且该“拐点”也为该函数的对称中心.若
的“拐点”。某同学经过探究发现:任何一个一元三次函数都有“拐点”;且该“拐点”也为该函数的对称中心.若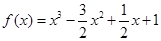 ,则
,则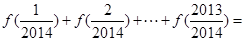 ( )
( )
| A.1 | B.2 | C.2013 | D.2014 |
推荐套卷
对于三次函数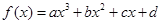
 ,给出定义:设
,给出定义:设 是函数
是函数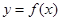 的导数,
的导数,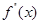 是函数
是函数 的导数,若方程
的导数,若方程 有实数解
有实数解 ,则称点
,则称点 为函数
为函数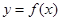 的“拐点”。某同学经过探究发现:任何一个一元三次函数都有“拐点”;且该“拐点”也为该函数的对称中心.若
的“拐点”。某同学经过探究发现:任何一个一元三次函数都有“拐点”;且该“拐点”也为该函数的对称中心.若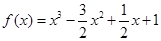 ,则
,则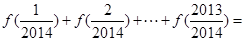 ( )
( )
| A.1 | B.2 | C.2013 | D.2014 |