实践操作:如图,△ABC是直角三角形,∠ACB=900,利用直尺和圆规按下列要求作图,并在图中表明相应的字母。(保留痕迹,不写作法)
(1)作BAC的平分线,交BC于点O;
(2)以O为圆心,OC为半径作圆。
综合运用:在你所作的图中,
(1)AB与⊙O的位置关系是 ;(直接写出答案)
(2)若AC=5,BC=12,求⊙O的半径。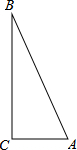
相关知识点
推荐套卷
实践操作:如图,△ABC是直角三角形,∠ACB=900,利用直尺和圆规按下列要求作图,并在图中表明相应的字母。(保留痕迹,不写作法)
(1)作BAC的平分线,交BC于点O;
(2)以O为圆心,OC为半径作圆。
综合运用:在你所作的图中,
(1)AB与⊙O的位置关系是 ;(直接写出答案)
(2)若AC=5,BC=12,求⊙O的半径。