春雷中学要了解全校学生对不同类别电视节目的喜爱情况,围绕“在体育、新闻、动画、娱乐四类电视节目中,你最喜欢哪一类?(必选且只选一类)”的问题,在全校范围内随机抽取部分学生进行问卷调查.将调查结果整理后绘制成如图所示的不完整的条形统计图.其中最喜欢新闻类电视节目的人数占被抽取人数的l0%.请你根据以上信息回答下列问题:
(1)在这次调查中,最喜欢新闻类电视节目的学生有多少名?并补全条形统计图:
(2)如果全校共有l 200名学生,请你估计全校学生中最喜欢体育类电视节目的学生有多少名?
相关知识点
推荐套卷

 与x轴交于A、B两点(A点在B点左侧),与y轴交于点C,对称轴为直线
与x轴交于A、B两点(A点在B点左侧),与y轴交于点C,对称轴为直线 ,OA = 2,OD平分∠BOC交抛物线于点D(点D在第一象限).
,OA = 2,OD平分∠BOC交抛物线于点D(点D在第一象限).
 在“传箴言”活动中,某班团支部对该班全体团员在一个月内所发箴言条数的情况进行了统计,并制成了如下两幅不完整的统计图:
在“传箴言”活动中,某班团支部对该班全体团员在一个月内所发箴言条数的情况进行了统计,并制成了如下两幅不完整的统计图:
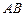 与
与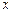 轴交于点A (– 2,0),与反比例函数在第一象限内的图象交于点B (2,n),连结BO,若
轴交于点A (– 2,0),与反比例函数在第一象限内的图象交于点B (2,n),连结BO,若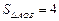 .
.
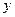 轴的交点为C,求△OCB的面积.
轴的交点为C,求△OCB的面积. 粤公网安备 44130202000953号
粤公网安备 44130202000953号