箱中有3个黑球，6个白球，每个球被取到的概率相同，
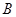箱中没有球．我们把从箱中取1个球放入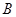箱中，然后在箱中补上1个与取走的球完全相同的球，称为一次操作，这样进行三次操作．
（1）分别求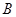箱中恰有1个、2个、3个白球的概率；
（2）从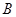箱中一次取出2个球，记白球的个数为
，求的分布列与数学期望．
的最小正周期及在区间
上的最大值和最小值；
，求
的值。
，
，其中
．
与
互相垂直；
与
的值(
为非零的常数)．
。
的定义域为
，
时，求
的单调区间；
为何值时，
，
夹角相等的单位向量
的坐标推荐套卷
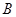箱中有3个黑球，6个白球，每个球被取到的概率相同，箱中没有球．我们把从箱中取1个球放入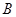箱中，然后在箱中补上1个与取走的球完全相同的球，称为一次操作，这样进行三次操作．
（1）分别求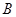箱中恰有1个、2个、3个白球的概率；
（2）从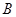箱中一次取出2个球，记白球的个数为，求的分布列与数学期望．
粤公网安备 44130202000953号