已知两点F1(-1,0)及F2(1,0),点P在以F1、F2为焦点的椭圆C上,且|PF1|、|F1F2|、|PF2|构成等差数列.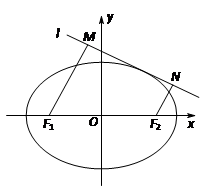
（1）求椭圆C的方程;
（2）如图,动直线l:y=kx+m与椭圆C有且仅有一个公共点,点M,N是直线l上的两点,且F1M⊥l, F2N⊥l.求四边形F1MNF2面积S的最大值.
)＋B，且f(
)＝7，f(π)－f(0)＝2
，求f(x).
的值.
的定义域.
－α)＝
，求cos(
π＋α)＋sin2(α－
，求f(α)的值；推荐套卷
已知两点F1(-1,0)及F2(1,0),点P在以F1、F2为焦点的椭圆C上,且|PF1|、|F1F2|、|PF2|构成等差数列.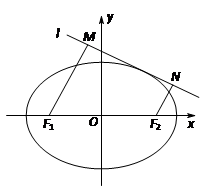
（1）求椭圆C的方程;
（2）如图,动直线l:y=kx+m与椭圆C有且仅有一个公共点,点M,N是直线l上的两点,且F1M⊥l, F2N⊥l.求四边形F1MNF2面积S的最大值.
粤公网安备 44130202000953号