解答一个问题后,将结论作为条件之一,提出与原问题有关的新问题,我们把它称为原问题的一个“逆向”问题.例如,原问题是“长方形的长和宽的长分别是3和4,求长方形的周长”,求出周长等于14后,它的一个“逆向”问题可以是“若长方形的周长为14,且一边长为3,求另一边的长”;也可以是“若长方形的周长为14,求长方形面积的最大值”,等等.
(1)设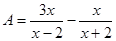 ,
,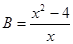 ,求A与B的积;
,求A与B的积;
(2)提出(1)的一个“逆向”问题,并解答这个问题.
相关知识点
推荐套卷
解答一个问题后,将结论作为条件之一,提出与原问题有关的新问题,我们把它称为原问题的一个“逆向”问题.例如,原问题是“长方形的长和宽的长分别是3和4,求长方形的周长”,求出周长等于14后,它的一个“逆向”问题可以是“若长方形的周长为14,且一边长为3,求另一边的长”;也可以是“若长方形的周长为14,求长方形面积的最大值”,等等.
(1)设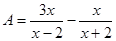 ,
,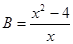 ,求A与B的积;
,求A与B的积;
(2)提出(1)的一个“逆向”问题,并解答这个问题.