下列命题中正确的是
（1）已知
为纯虚数的充要条件
（2）当
是非零 实数时，
恒成立
（3）复数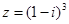
的实部和虚部都是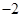
（4）设的共轭复数为
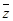，若
| A．（1）（2） | B．（1）（3） | C．（2）（3） | D．（2）（4） |
的对边分别为
，若
，则
（）
的前n项和为48，前2n项和为60，则前3n项和为（）
中,若
，则
（）
中，
，
，
，则
等于（）
是数列
中的第（）项.
相关知识点
推荐套卷
下列命题中正确的是
（1）已知为纯虚数的充要条件
（2）当是非零 实数时，恒成立
（3）复数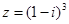的实部和虚部都是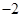
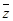（4）设的共轭复数为，若
| A．（1）（2） | B．（1）（3） | C．（2）（3） | D．（2）（4） |
粤公网安备 44130202000953号