已知抛物线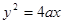 (
(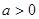 且
且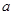 为常数),
为常数),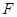 为其焦点.
为其焦点.
(1)写出焦点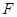 的坐标;
的坐标;
(2)过点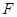 的直线与抛物线相交于
的直线与抛物线相交于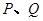 两点,且
两点,且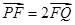 ,求直线
,求直线 的斜率;
的斜率;
(3)若线段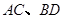 是过抛物线焦点
是过抛物线焦点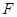 的两条动弦,且满足
的两条动弦,且满足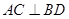 ,如图所示.求四边形
,如图所示.求四边形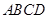 面积的最小值
面积的最小值 .
.
推荐套卷
已知抛物线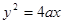 (
(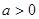 且
且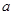 为常数),
为常数),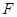 为其焦点.
为其焦点.
(1)写出焦点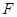 的坐标;
的坐标;
(2)过点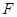 的直线与抛物线相交于
的直线与抛物线相交于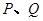 两点,且
两点,且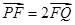 ,求直线
,求直线 的斜率;
的斜率;
(3)若线段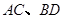 是过抛物线焦点
是过抛物线焦点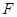 的两条动弦,且满足
的两条动弦,且满足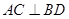 ,如图所示.求四边形
,如图所示.求四边形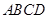 面积的最小值
面积的最小值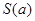 .
.