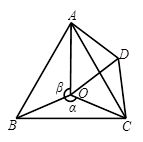
如图,点 是等边
是等边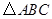 内一点,
内一点,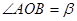 ,
, 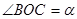 .将
.将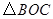 绕点
绕点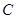 按顺时针方向旋转
按顺时针方向旋转 得
得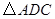 ,连接
,连接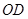 .
.
(1)当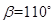 ,
,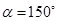 时,试判断
时,试判断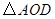 的形状,并说明理由.
的形状,并说明理由.
(2)请写出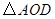 是等边三角形时
是等边三角形时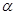 、
、 的度数.
的度数.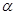 = 度;
= 度;  = 度.
= 度.
(3)探究:若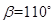 ,则
,则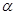 为多少度时,
为多少度时,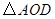 是等腰三角形?
是等腰三角形?
(只要写出探究结果)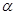 = ;
= ;
相关知识点
推荐套卷
如图,点 是等边
是等边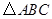 内一点,
内一点,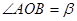 ,
, 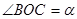 .将
.将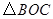 绕点
绕点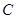 按顺时针方向旋转
按顺时针方向旋转 得
得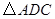 ,连接
,连接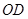 .
.
(1)当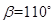 ,
,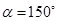 时,试判断
时,试判断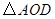 的形状,并说明理由.
的形状,并说明理由.
(2)请写出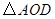 是等边三角形时
是等边三角形时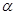 、
、 的度数.
的度数.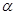 = 度;
= 度;  = 度.
= 度.
(3)探究:若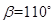 ,则
,则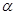 为多少度时,
为多少度时,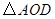 是等腰三角形?
是等腰三角形?
(只要写出探究结果)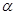 = ;
= ;