如图是某货站传送货物的平面示意图,AD与地面的夹角为60°,为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°变成37°,因此传送带的落地点由点B到点C向前移动了2米.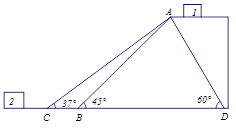
(1)求点A与地面的高度;
(2)如果需要在货物着地点C的左侧留出2米,那么请判断距离D点14米的货物2是否需要挪走,并说明理由.(sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,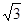 ≈1.73)
≈1.73)
相关知识点
推荐套卷
如图是某货站传送货物的平面示意图,AD与地面的夹角为60°,为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°变成37°,因此传送带的落地点由点B到点C向前移动了2米.
(1)求点A与地面的高度;
(2)如果需要在货物着地点C的左侧留出2米,那么请判断距离D点14米的货物2是否需要挪走,并说明理由.(sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,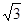 ≈1.73)
≈1.73)