补全证明过程
已知：如图，∠1＝∠2，∠C＝∠D。
求证：∠A＝∠F。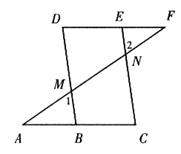
证明：∵∠1＝∠2（已知），
又∠1＝∠DMN（___________________），
∴∠2＝∠_________（等量代换）。
∴DB∥EC（同位角相等，两直线平行）。
∴∠A＝∠F（两直线平行，内错角相等）。
相关试题
某市今年计划修建一段全长1500米的景观路，为了尽量减少施工对城市交通的影响，实际施工时，每天的工效比原计划增加20%，结果提前2天完成这一任务，求原计划每天修路多少米？
； （2）
.如图9，在平面直角坐标系xOy中,矩形ABCD的AB边在x轴上，且AB=3,AD=2,经过点C的直线y=x-2与x轴、y轴分别交于点E、F.
（1）求矩形ABCD的顶点A、B、C、D的坐标；
（2）求证：△OEF≌△BEC；
（3）P为直线y=x-2上一点，若S△POE=5，求点P的坐标.
（10分)如图8, △ABC是等边三角形，D是BC延长线上任意一点，以AD为一边向右侧作等边△ADE，连接CE.
（1）求证：△CAE≌△BAD；
（2）判断直线AB与EC的位置关系，并说明理由.
两个函数的图象；
粤公网安备 44130202000953号