为了解学生身高情况，某校以10%的比例对全校700名学生按性别进行分层抽样调查，测得身高情况的统计图如下：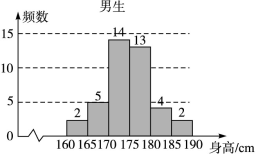
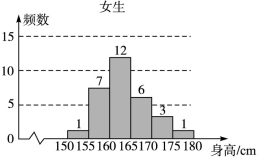
(Ⅰ)估计该校男生的人数；
(Ⅱ)估计该校学生身高在170～185 cm之间的概率；
(Ⅲ)从样本中身高在180～190 cm之间的男生中任选2人，求至少有1人身高在185～190 cm之间的概率．
相关试题
上有点
，用定义求：
处的切线的斜率；
上一点
的切线方程。
，
，其中
为常数。
在点
处的切线的斜率和切线方程；
的图象过点
的图象与
中切线的交点。
，求该物体在
时的瞬时速度；（2）已知
，求该物体在
与直线
，求：（1）两曲线的交点；（2）抛物线在交点处的切线方程。相关知识点
推荐套卷
为了解学生身高情况，某校以10%的比例对全校700名学生按性别进行分层抽样调查，测得身高情况的统计图如下：
(Ⅰ)估计该校男生的人数；
(Ⅱ)估计该校学生身高在170～185 cm之间的概率；
(Ⅲ)从样本中身高在180～190 cm之间的男生中任选2人，求至少有1人身高在185～190 cm之间的概率．
粤公网安备 44130202000953号