在进行一项掷骰子放球游戏中，规定：若掷出1点，甲盒中放一球；
若掷出2点或3点，乙盒中放一球；若掷出4点或5点或6点，丙盒中放一球，前后共掷3
次，设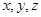
分别表示甲，乙，丙3个盒中的球数.
（1）求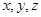依次成公差大于0的等差数列的概率；
（2）记
，求随机变量
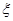的概率分布列和数学期望.
在[1,4]上的单调性并求其最值.
在
上恒有
<2，求
的取值范围．
在R上为奇函数，当
，求
；
，
，
.
，求实数
的值；
且
，求实数
，实数推荐套卷
在进行一项掷骰子放球游戏中，规定：若掷出1点，甲盒中放一球；
若掷出2点或3点，乙盒中放一球；若掷出4点或5点或6点，丙盒中放一球，前后共掷3
次，设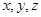分别表示甲，乙，丙3个盒中的球数.
（1）求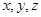依次成公差大于0的等差数列的概率；
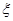（2）记，求随机变量的概率分布列和数学期望.
粤公网安备 44130202000953号