如图，一抛物线经过点A、B、C，点 A（−2，0），点B（0，4），点C（4，0），该抛物线的顶点为D．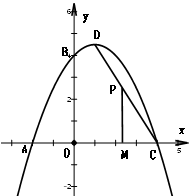
（1）求该抛物线的解析式及顶点D坐标；
（2）如图，若P为线段CD上的一个动点，过点P作PM⊥x轴于点M，求四边形PMAB的面积的最大值和此时点P的坐标；
（3）过抛物线顶点D，作DE⊥x轴于E点，F（m，0）是x轴上一动点，若以BF为直径的圆与线段DE有公共点，求m的取值范围．
已知：在△ABC中，AB=6，BC=8，AC=10，O为AB边上的一点，以O为圆心，OA长为半径作圆交AC于D点，过D作⊙O的切线交BC于E.
（1）若O为AB的中点(如图1)，则ED与EC的大小关系为：ED EC（填“
”“
”或“
”）
（2）若OA<3时（如图2），（1）中的关系是否还成立？为什么？
（3）当⊙O过BC中点时（如图3），求CE长.
如图，把两个全等的Rt△AOB和Rt△COD分别置于平面直角坐标系中，使直角边OB、OD在x轴上．已知点A（1，2）在二次函数y=ax2+(a+5)x的图象上．
（1）求该二次函数的关系式；
（2）点C是否在此二次函数的图象上，说明理由；
（3）若点P为直线OC上一个动点，过点P作y轴的平行线交抛物线于点M，问是否存在这样的点P，使得四边形ABMP为平行四边形？若存在，求出此时点P的坐标；若不存在，请说明理由．
已知：E、F是矩形ABCD的对角线AC上的两点，且AE=CF=
，连接DE并延长交AB于M，连接BF交CD于N，
（1）求证：四边形BMDN是平行四边形；
（2）当四边形BMDN是菱形时，求
的值.
在锐角△ABC中，AB=4，BC=5，∠ACB=45°，将△ABC绕点B按逆时针方向旋转，得到△A1BC1．
（1）当点C1在线段CA的延长线上时，如图1，求∠CC1A1的度数；
（2）如图2，△ABC绕点B按逆时针方向旋转，连接AA1，CC1，若△ABA1的面积为4，求△CBC1的面积；
（3）点E为线段AB中点，点P是线段AC上的动点，在△ABC绕点B按逆时针方向旋转过程中，点P的对应点是点P1，求线段EP1长度的最大值与最小值．
个单位后其顶点恰好在y轴上，求抛物线C的解析式及其上的不动点；
成立？若存在，求出k的值；若不存在，请说明理由.
粤公网安备 44130202000953号