某中学综合实践活动组为了解学生最喜欢的球类运动，对足球、乒乓球、篮球、排球四个项目进行了调查，并将调查的结果绘制成如下的两幅统计图（说明：每位同学只选一种自己最喜欢的球类），请你根据图中提供的信息解答下列问题：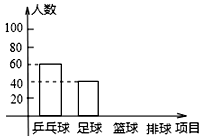
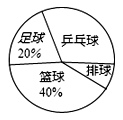
（1）求这次接受调查的学生人数，并补全条形统计图；
（2）求扇形统计图中喜欢排球的圆心角度数；
（3）若调查到爱好“乒乓球”的5名学生中有3名男生，2名女生，现从这5名学生中任意抽取2名学生，请用列表法或画树状图的方法，求出刚好抽到一男一女的概率．
(12分)2007年我市某县筹备20周年县庆，园林部门决定利用现有的3490盆甲种花卉和295
0盆乙种花卉搭配
两种园艺造型共50个摆放在迎宾大道两侧，已知搭配一个
种造型需甲种花卉80盆，乙种花卉40盆，搭配一个
种造型需甲种花卉50盆，乙种花卉90盆.
（1）某校九年级（1）班课外活动小组承接了这个园艺造型搭配方案的设计，问符合题意的搭配方案有几种？请你帮助设计出来.
（2）若搭配一个种造型的成本是800元，搭配一个种造型的成本是960元，试说明（1）中哪种方案成本最低？最低成本是多少元？
.
(10分)今年春季，我国云南、贵州等西南地区遇到多少不遇旱灾，“一方有难，八方支援”，为及时灌溉农田，丰收农机公司决定支援上坪村甲、乙、丙三种不同功率柴油发电机共10台(每种至少一台)及配套相同型号抽水机4台、3台、2台，每台抽水机每小时可抽水灌溉农田1亩.现要求所有柴油发电机及配套抽水机同时工作一小时，灌溉农田32亩.
(1)设甲种柴油发电机数量为x台，乙种柴油发电机数量为y台.
①用含x、y的式子表示丙种柴油发电机的数量；
②求出y与x的关系式；
(2)已知甲、乙、丙柴油发电机每台每小时费用分别为130元、120元、100元，应如何安排三种柴油发电机的数量，既能按要求抽水灌溉，同时柴油发电机总费用W最少？
(10分)某学校组织八年级学生参加社会实践活动，若单独租用35座客车若干辆，则刚好坐满；若单独租用55座客车，则可以少租一辆，且余45个空座位.
(1)求该校八年级学生参加社会实践活动的人数；
(2)已知35座客车的租金为每辆320元，55座客车的租金为每辆400元.根据租车资金不超过1500元的预算，学校决定同时租用这两种客车共4辆(可以坐不满).请你计算本次社会实践活动所需车辆的租金.
＜1；⑶ 2x+3＞1；⑷ 0.2x－3＜－2.你喜欢其中哪两个不等式，请把它们选出来组成一个不等式组，求出它的解集，并在数轴上把解集表示出来
粤公网安备 44130202000953号