（1）已知正方形ABCD ，点E、F、G、H分别在边AB、BC、CD、DA上，若EG⊥FH，求证EG = FH”（如图1）；
（2）如果把条件中的“正方形”改为“长方形”，并设AB =2，BC =3（如图2），试探究EG、FH之间有怎样的数量关系，并证明你的结论；
（3）如果把条件中的“EG⊥FH”改为“EG与FH的夹角为45°”，并假设正方形ABCD的边长为1，FH的长为
（如图3），试求EG的长度。
相关试题
某批发商以每件50元的价格购进800件T恤，第一个月以单价80元销售，售出了200件；第二个月如果单价不变，预计仍可售出200件，批发商为增加销售量，决定降价销售，根据市场调查，单价每降低1元，可多售出10件，但最低单价应高于购进的价格；第二个月结束后，批发商将对剩余的T恤一次性清仓销售，清仓是单价为40元，设第二个月单价降低
元。
（1）填表（不需化简）
| 时间 |
第一个月 |
第二个月 |
清仓时 |
| 单价（元） |
80 |
40 |
|
| 销售量（件） |
200 |
（2）如果批发商希望通过销售这批T恤获利9000元，那么第二个月的单价应是多少元？
有一块两条直角边BC、AC的长分别为3厘米和4厘米的Rt△ABC的铁片，现要把它加工成一个面积尽最大的正方形，甲、乙两位师傅加工方案分别如图所示，请用你学过的知识说明哪位师傅的加工方案符合要求（加工中的损耗忽略不计）．
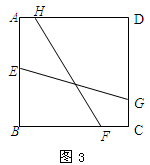
相关知识点
推荐套卷
粤公网安备 44130202000953号