课题研究小组对附着在物体表面的三个微生物(课题小组成员把他们分别标号为1,2,3)的生长情况进行观察记录.这三个微生物第一天各自一分为二,产生新的微生物(分别被标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象的记录).那么标号为100的微生物会出现在第 天.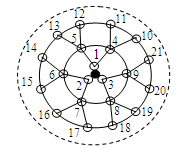
相关知识点
推荐套卷
课题研究小组对附着在物体表面的三个微生物(课题小组成员把他们分别标号为1,2,3)的生长情况进行观察记录.这三个微生物第一天各自一分为二,产生新的微生物(分别被标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象的记录).那么标号为100的微生物会出现在第 天.