某仓库有甲种货物360吨,乙种货物290吨,计划用A、B两种共50辆货车运往外地.已知一辆A种货车的运费需0.5万元,一辆B种货车的运费需0.8万元.
(1)设A种货车为 辆,运输这批货物的总运费为y万元,试写出y与
辆,运输这批货物的总运费为y万元,试写出y与 的关系表达式;
的关系表达式;
(2)若一辆A种货车能装载甲种货物9吨和乙种货物3吨;一辆B种货车能装载甲种货物6吨和乙种货物8吨.按此要求安排A,B两种货车运送这批货物,有哪几种运输方案?请设计出来;
(3)试说明哪种方案总运费最少?最少运费是多少万元?
相关知识点
推荐套卷
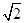 x2-(x+1)是关于x的一元二次方程?当m 取何值时,方程m(x2+x)=
x2-(x+1)是关于x的一元二次方程?当m 取何值时,方程m(x2+x)= 粤公网安备 44130202000953号
粤公网安备 44130202000953号