我国宋代数学家杨辉在1261年提到一个有意思的关于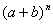 展开式中各项系数间的关系:
展开式中各项系数间的关系:
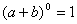 ,它只有一项,系数为1;
,它只有一项,系数为1;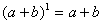 ,它有两项,系数为1、1;
,它有两项,系数为1、1;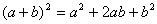 ,它有三项,系数为1、2、1;
,它有三项,系数为1、2、1;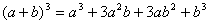 ,它有四项,系数为1、3、3、1;
,它有四项,系数为1、3、3、1;
如果把其系数按上图排列,得到一个三角形,我们把它叫杨辉三角,其规律的发现比欧洲早393年;那么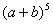 展开项的所有系数的和为 ( )
展开项的所有系数的和为 ( )
| A.16 | B.22 | C.32 | D.64 |
我国宋代数学家杨辉在1261年提到一个有意思的关于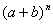 展开式中各项系数间的关系:
展开式中各项系数间的关系:
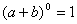 ,它只有一项,系数为1;
,它只有一项,系数为1;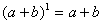 ,它有两项,系数为1、1;
,它有两项,系数为1、1;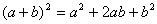 ,它有三项,系数为1、2、1;
,它有三项,系数为1、2、1;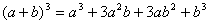 ,它有四项,系数为1、3、3、1;
,它有四项,系数为1、3、3、1;
如果把其系数按上图排列,得到一个三角形,我们把它叫杨辉三角,其规律的发现比欧洲早393年;那么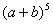 展开项的所有系数的和为 ( )
展开项的所有系数的和为 ( )
| A.16 | B.22 | C.32 | D.64 |