对于定义在实数集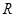 上的两个函数
上的两个函数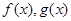 ,若存在一次函数
,若存在一次函数 使得,对任意的
使得,对任意的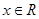 ,都有
,都有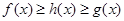 ,则把函数
,则把函数 的图像叫函数
的图像叫函数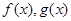 的“分界线”。现已知
的“分界线”。现已知 (
(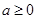 ,
, 为自然对数的底数),
为自然对数的底数),
(1)求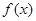 的递增区间;
的递增区间;
(2)当 时,函数
时,函数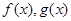 是否存在过点
是否存在过点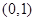 的“分界线”?若存在,求出函数
的“分界线”?若存在,求出函数 的解析式,若不存在,请说明理由。
的解析式,若不存在,请说明理由。
相关知识点
推荐套卷
对于定义在实数集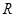 上的两个函数
上的两个函数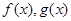 ,若存在一次函数
,若存在一次函数 使得,对任意的
使得,对任意的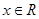 ,都有
,都有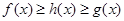 ,则把函数
,则把函数 的图像叫函数
的图像叫函数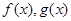 的“分界线”。现已知
的“分界线”。现已知 (
(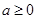 ,
, 为自然对数的底数),
为自然对数的底数),
(1)求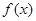 的递增区间;
的递增区间;
(2)当 时,函数
时,函数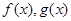 是否存在过点
是否存在过点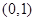 的“分界线”?若存在,求出函数
的“分界线”?若存在,求出函数 的解析式,若不存在,请说明理由。
的解析式,若不存在,请说明理由。