如图，正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦，AE垂直于圆O所在平面，垂足E是圆O上异于C、D的点，AE=3，正方形ABCD的边长为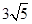
．
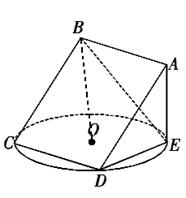
（1）求证：平面ABCD丄平面ADE；
（2）求四面体BADE的体积；
（3）试判断直线OB是否与平面CDE垂直，并请说明理由．
相关试题
是递增数列，
，数列
满足
，且
（
）
是等差数列；
总成立，求实数
的最大值．
，函数
的图象关于点
对称．
时，求
且
，求△ABC的面积．
，当
时满足
，
，求数列
的前n项和
．
的部分图象如图所示．
的解析式，并写出
的内角分别是A，B，C，角A为锐角，且
的值．
为实数，函数
时，求
在
上的最大值； 
，当
有两个极值点
时，总有
，求实数
的值。（
为推荐套卷
如图，正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦，AE垂直于圆O所在平面，垂足E是圆O上异于C、D的点，AE=3，正方形ABCD的边长为．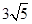
（1）求证：平面ABCD丄平面ADE；
（2）求四面体BADE的体积；
（3）试判断直线OB是否与平面CDE垂直，并请说明理由．
粤公网安备 44130202000953号