如图,在平面直角坐标系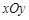 中,
中,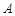 、
、 为
为 轴上两点,
轴上两点,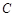 、
、 为
为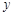 一上两点,经过点
一上两点,经过点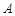 、
、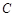 、
、 的抛物线的一部分
的抛物线的一部分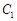 与经过点
与经过点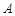 、
、
 的抛物线的一部分
的抛物线的一部分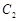 组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点
组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点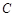 的坐标为
的坐标为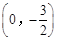 ,点
,点 是抛物线
是抛物线 的顶点.
的顶点.
(1)求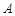 、
、 两点的坐标;
两点的坐标;
(2)“蛋线”在第四象限上是否存在一点 ,使得
,使得 的面积最大?若存在,求出
的面积最大?若存在,求出 面积的最大值;若不存在,请说明理由;
面积的最大值;若不存在,请说明理由;
(3)当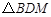 为直角三角形时,求
为直角三角形时,求 的值.
的值.
相关知识点
推荐套卷
如图,在平面直角坐标系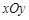 中,
中,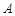 、
、 为
为 轴上两点,
轴上两点,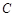 、
、 为
为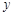 一上两点,经过点
一上两点,经过点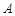 、
、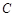 、
、 的抛物线的一部分
的抛物线的一部分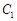 与经过点
与经过点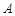 、
、
 的抛物线的一部分
的抛物线的一部分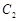 组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点
组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点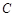 的坐标为
的坐标为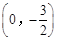 ,点
,点 是抛物线
是抛物线 的顶点.
的顶点.
(1)求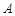 、
、 两点的坐标;
两点的坐标;
(2)“蛋线”在第四象限上是否存在一点 ,使得
,使得 的面积最大?若存在,求出
的面积最大?若存在,求出 面积的最大值;若不存在,请说明理由;
面积的最大值;若不存在,请说明理由;
(3)当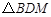 为直角三角形时,求
为直角三角形时,求 的值.
的值.