如图所示是某水产养殖厂的养殖大网箱的平面图，四周的实线为网衣，为避免混养，
（1）若大网箱的面积为108平方米，每个小网箱的横边
、纵边
设计为多少米时，才能使围成的网箱中筛网的总长度最小？
（2）若大网箱的面积为160平方米，网衣的造价为112元/米，筛网的造价为96元/米，且大网箱的长与宽都不超过15米，则小网箱的横、纵边分别为多少米时，可使总造价最低？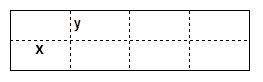
，求f（x）和g（x）的解析式。
；
的取值范围.
;
，
，求
。
的函数
在区间
上的值域为
，
、
的值；
的最小正周期；
在
上的最大值
的值。推荐套卷
如图所示是某水产养殖厂的养殖大网箱的平面图，四周的实线为网衣，为避免混养，
（1）若大网箱的面积为108平方米，每个小网箱的横边、纵边设计为多少米时，才能使围成的网箱中筛网的总长度最小？
（2）若大网箱的面积为160平方米，网衣的造价为112元/米，筛网的造价为96元/米，且大网箱的长与宽都不超过15米，则小网箱的横、纵边分别为多少米时，可使总造价最低？
粤公网安备 44130202000953号