某电子厂商投产一种新型电子产品，每件制造成本为18元，试销过程中发现，每月销售量
（万件）与销售单价
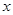（元）之间的关系可以近似地看作一次函数
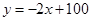．（利润=售价-制造成本）
（1）写出每月的利润
（万元）与销售单价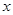（元）之间的函数关系式；
（2）当销售单价为多少元时，厂商每月获得的利润为440万元？
（3）根据相关部门规定，这种电子产品的销售单价不能高于40元，如果厂商每月的制造成本不超过540万元，那么当销售单价为多少元时，厂商每月获得的利润最大？最大利润为多少万元？
相关试题
)÷
，然后在0，1，－1中挑选一个合适的数代入求值．
；
.(本题满分12分)已知
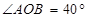，∠AOB的余角为∠AOC，∠AOB的补角为∠BOD，OM平分∠AOC， ON平分∠BOD．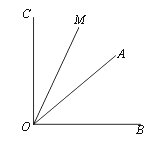
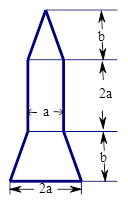
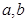（1）如图，当射线OM在∠AOB的外部时，用直尺、量角器画出射线OD，ON的准确位置；
（2）求（1）中∠MON的度数，要求写出计算过程；
解：
(本题满分12分)现在，友谊商场进行促销活动，出售一种优惠购物卡（注：此卡只作为购物优惠凭证不能顶替货款），花300元买这种卡后，凭卡可在这家商场按标价的8折购物.
（1）顾客购买多少元金额的商品时，买卡与不买卡花钱相等？在什么情况下购物合算？
（2）小张要买一台标价为3500元的冰箱，如何购买合算？小张能节省多少元钱？
（3）小张按合算的方案，把这台冰箱买下，如果友谊商场还能盈利25％，这台冰箱的进价是多少元？
的式子表示该截面的面积
；
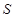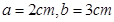时，求这个火箭模型截面的面积.相关知识点
推荐套卷
粤公网安备 44130202000953号