如图,某人在一栋高层建筑顶部C处测得山坡坡脚A处的俯角为60°,又测得山坡上一棵小树树干与坡面交界P处的俯角为45°,已知OA=50米,山坡坡度为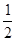 (即tan∠PAB=
(即tan∠PAB=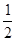 ,其中PB⊥AB ),且O、A、B在同一条直线上.
,其中PB⊥AB ),且O、A、B在同一条直线上. 
(1)求此高层建筑的高度OC.(结果保留根号形式.);
(2)求坡脚A处到小树树干与坡面交界P处的坡面距离AP的长度. (人的高度及测量仪器高度忽略不计,结果保留根号形式.)
相关知识点
推荐套卷
如图,某人在一栋高层建筑顶部C处测得山坡坡脚A处的俯角为60°,又测得山坡上一棵小树树干与坡面交界P处的俯角为45°,已知OA=50米,山坡坡度为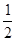 (即tan∠PAB=
(即tan∠PAB=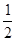 ,其中PB⊥AB ),且O、A、B在同一条直线上.
,其中PB⊥AB ),且O、A、B在同一条直线上. 
(1)求此高层建筑的高度OC.(结果保留根号形式.);
(2)求坡脚A处到小树树干与坡面交界P处的坡面距离AP的长度. (人的高度及测量仪器高度忽略不计,结果保留根号形式.)