某超市经销一种销售成本为每件30元的商品.据市场调查分析,如果按每件40元
销售,一周能售出500件,若销售单价每涨1元,每周的销售量就减少10件.设销售单价为每件x元(x≥40),一周的销售量为y件.
(1)写出y与x的函数关系式(标明x的取值范围);
(2)设一周的销售利润为s元,写出s与x的函数关系式,并确定当单价在什么范围内变化时,
利润随着单价的增大而增大;
(3)在超市对该种商品投入不超过8800元的情况下,使得一周销售利润达到8000元,销售单价应定为多少?
相关知识点
推荐套卷
 的解x和y的绝对值相等,试求a的值.
的解x和y的绝对值相等,试求a的值.
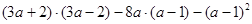 (其中:
(其中: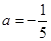 )
)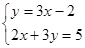
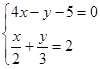
 粤公网安备 44130202000953号
粤公网安备 44130202000953号