设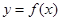
为区间
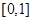上的连续函数，且恒有
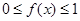，可以用随机模拟方法近似计算由曲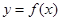线及直线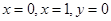
所围成部分的面积
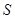，先产生两组（每组N个）区间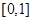上的均匀随机数
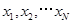和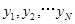
，由此得到N个点
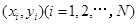，再数出其中满足
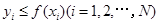的点数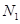
，那么由随机模拟方案可得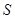的近似值为 。
相关试题
的定义域是[－2，0]，则f(x)的单调递减区间是____．
，当x∈(－2，＋∞)时，是增函数，当x∈(－∞，－2)时是减函数，则f(1)＝________．
－ａｘ－ｂ的两个零点分别为２和３，则函数ｇ（ｘ）＝ｂ
－２ｘ－３ｋ＝０的两根一个大于１，一个小于１，则实数的取值范围 ．
－６＝０的近似解（精确到０.０１）是 ．相关知识点
推荐套卷
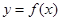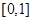设为区间上的连续函数，且恒有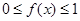，可以用随机模拟方法近似计算由曲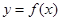线及直线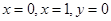所围成部分的面积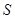，先产生两组（每组N个）区间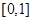上的均匀随机数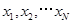和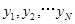，由此得到N个点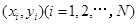，再数出其中满足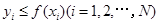的点数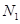，那么由随机模拟方案可得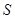的近似值为 。
粤公网安备 44130202000953号