研究问题:“已知关于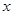 的不等式
的不等式 的解集为(1,2),解关于
的解集为(1,2),解关于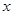 的
的
不等式 ”,有如下解法:由
”,有如下解法:由 ,令
,令 ,则
,则 ,所以不等式
,所以不等式 的解集为
的解集为 。类比上述解法,已知关于
。类比上述解法,已知关于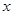 的不等式
的不等式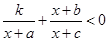 的解集为
的解集为 ,则关于
,则关于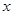 的不等式
的不等式 的解集
的解集
为 .
推荐套卷
研究问题:“已知关于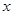 的不等式
的不等式 的解集为(1,2),解关于
的解集为(1,2),解关于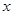 的
的
不等式 ”,有如下解法:由
”,有如下解法:由 ,令
,令 ,则
,则 ,所以不等式
,所以不等式 的解集为
的解集为 。类比上述解法,已知关于
。类比上述解法,已知关于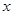 的不等式
的不等式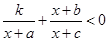 的解集为
的解集为 ,则关于
,则关于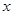 的不等式
的不等式 的解集
的解集
为 .