（1）解不等式组．并把解集在数轴上表示出来．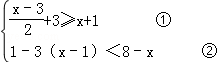
．
（2）阅读某同学解分式方程的具体过程，回答后面问题．
解方程
．
解：原方程可化为：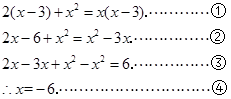
检验：当
时，各分母均不为0，
∴是原方程的解．
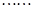⑤
请回答：（1）第①步变形的依据是____________________；
（2）从第____步开始出现了错误，这一步错误的原因是__________________________；
（3）原方程的解为____________________________．
相关试题
已知某工厂计划用库存的302m3木料为某学校生产500套桌椅，供该校1250名学生使用，该厂生产的桌椅分为A，B两种型号，有关数据如下：
| 桌椅型号 |
一套桌椅所坐学生人数（单位：人） |
生产一套桌椅所需木材（单位：m3） |
一套桌椅的生产成本（单位：元） |
一套桌椅的运费（单位：元） |
| A |
2 |
0.5 |
100 |
2 |
| B |
3 |
0.7 |
120 |
4 |
设生产A型桌椅x（套），生产全部桌椅并运往该校的总费用（总费用=生产成本+运费）为y元．
（1）求y与x之间的关系式，并指出x的取值范围；
（2）当总费用y最小时，求相应的x值及此时y的值．
如图，在▱ABCD中，E，F分别为BC，AB中点，连接FC，AE，且AE与FC交于点G，AE的延长线与DC的延长线交于点N．
（1）求证：△ABE≌△NCE；
（2）若AB=3n，FB=
GE，试用含n的式子表示线段AN的长．
如图，在△AOB中，∠ABO=90°，OB=4，AB=8，反比例函数y=
在第一象限内的图象分别交OA，AB于点C和点D，且△BOD的面积S△BOD=4．
（1）求反比例函数解析式；
（2）求点C的坐标．
相关知识点
推荐套卷
粤公网安备 44130202000953号