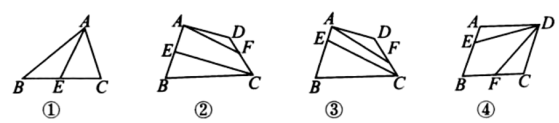
(1)如图①,
的面积是
,点
是
的中点,连接
的面积是_____.
(2)如图②,四边形
的面积是
,点
分别是一组对边
的中点,连接
,则四边形
的面积是_____.
(3)如图③,点
分别是一组对边
上的点,且
,若四边形
的面积是
,连接
,则四边形
的面积是_____.
(4)如图④,
的面积是
,点
从点
出发沿
以每秒
个单位长的速度向点
运动,点
从点
出发沿
以每秒
个单位长的速度向点
运动.点
分别从点
同时出发,当其中一点到达端点时,另一点也随之停止运动.请问四边形
的面积的值是否随着时间
的变化而变化?若不变,请求出这个值;若变化,说明怎样变化的.