某中学为落实市教育局提出的“全员育人,创办特色学校”的会议精神,决心打造“书香校园”,计划用不超过1900本科技类书籍和1620本人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本.
(1)符合题意的组建方案有几种?请你帮学校设计出来;
(2)若组建一个中型图书角的费用是860元,组建一个小型图书角的费用是570
元,试说明(1)中哪种方案费用最低,最低费用是多少元?
相关知识点
推荐套卷
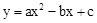 的一个交点为A(0,2),同时这条直线与x轴相交于点B,且相交所成的角β为45°.
的一个交点为A(0,2),同时这条直线与x轴相交于点B,且相交所成的角β为45°.
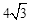 ,直角边CD在y轴上,且点C与点A重合.Rt△CDE沿y轴正方向平行移动,当点C运动到点O时停止运动.解答下列问题:
,直角边CD在y轴上,且点C与点A重合.Rt△CDE沿y轴正方向平行移动,当点C运动到点O时停止运动.解答下列问题: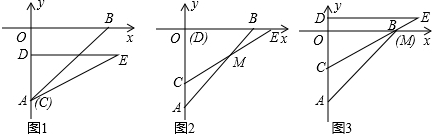

 OABC一起先向右平移4个单位后,再向下平移m(0<m<3)个单位,得到抛物线W′和
OABC一起先向右平移4个单位后,再向下平移m(0<m<3)个单位,得到抛物线W′和 (a>0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,点D的坐标为(﹣6,0),且∠ACD=90°.
(a>0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,点D的坐标为(﹣6,0),且∠ACD=90°.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号