列方程解应用题
某公司2013年计划在甲、乙两个电视台播放总时长为300分钟的广告,已知甲、乙两电视台的广告收费标准分别为500元/分钟和200元/分钟,该公司2013年的广告总费用计划为9万元。
(1)求:该公司2013年计划在甲、乙两个电视台播放广告的时长分别为多少分钟?
(2)如果甲、乙两个电视台播放该公司的广告,预计能给该公司分别带来0.3万元/分钟和0.2万元/分钟的收益。求:甲、乙两个电视台2013年为该公司播放广告,预计将能给该公司带来的总收益是多少万元?
相关知识点
推荐套卷

 的一元二次方程
的一元二次方程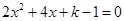 有实数根,
有实数根, 为正整数.
为正整数.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号