学校门口经常有小贩搞摸奖活动．某小贩在一只黑色的口袋里装有只有颜色不同的50只小球，其中红球1只，黄球2只，绿球10只，其余为白球．搅拌均匀后，每2元摸1个球．奖品的情况标注在球上（如下图）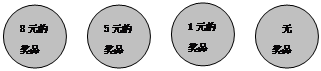
（1）如果花2元摸1个球，那么摸不到奖的概率是多少？
（2）如果花4元同时摸2个球，那么获得10元奖品的概率是多少？
学校门口经常有小贩搞摸奖活动．某小贩在一只黑色的口袋里装有只有颜色不同的50只小球，其中红球1只，黄球2只，绿球10只，其余为白球．搅拌均匀后，每2元摸1个球．奖品的情况标注在球上（如下图）
（1）如果花2元摸1个球，那么摸不到奖的概率是多少？
（2）如果花4元同时摸2个球，那么获得10元奖品的概率是多少？
，求这个正方体的表面积（结果保留4个有效数字）
，你能从中找出计算规律吗？如果将根号内的数10换成
，这种计算规律是否仍然存在，你能用公式表示上述计算规律吗？
和
的大小.
；（2）
；（3）
；（4）
，求正方体的棱长（保留3个有效数字）
粤公网安备 44130202000953号