下列命题中,真命题的有 ______ 。(只填写真命题的序号)
① 若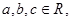 则“
则“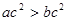 ”是“
”是“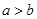 ”成立的充分不必要条件;
”成立的充分不必要条件;
② 当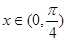 时,函数
时,函数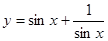 的最小值为2;
的最小值为2;
③ 若命题“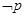 ”与命题“
”与命题“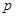 或
或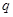 ”都是真命题,则命题
”都是真命题,则命题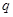 一定是真命题;
一定是真命题;
④ 若命题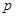 :
: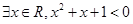 ,则
,则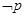 :
: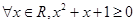 .
.
推荐套卷
下列命题中,真命题的有 ______ 。(只填写真命题的序号)
① 若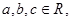 则“
则“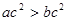 ”是“
”是“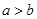 ”成立的充分不必要条件;
”成立的充分不必要条件;
② 当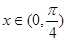 时,函数
时,函数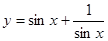 的最小值为2;
的最小值为2;
③ 若命题“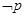 ”与命题“
”与命题“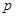 或
或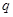 ”都是真命题,则命题
”都是真命题,则命题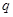 一定是真命题;
一定是真命题;
④ 若命题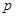 :
: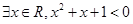 ,则
,则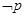 :
: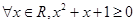 .
.