(本小题满分13分)
已知 ,
, 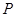 是平面上一动点,
是平面上一动点, 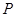 到直线
到直线 上的射影为点
上的射影为点 ,且满足
,且满足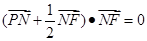
(Ⅰ)求点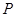 的轨迹
的轨迹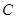 的方程;
的方程;
(Ⅱ)过点 作曲线
作曲线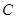 的两条弦
的两条弦 , 设
, 设 所在直线的斜率分别为
所在直线的斜率分别为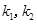 , 当
, 当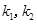 变化且满足
变化且满足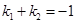 时,证明直线
时,证明直线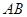 恒过定点,并求出该定点坐标.
恒过定点,并求出该定点坐标.
推荐套卷
(本小题满分13分)
已知 ,
, 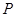 是平面上一动点,
是平面上一动点, 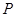 到直线
到直线 上的射影为点
上的射影为点 ,且满足
,且满足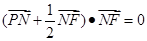
(Ⅰ)求点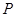 的轨迹
的轨迹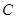 的方程;
的方程;
(Ⅱ)过点 作曲线
作曲线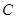 的两条弦
的两条弦 , 设
, 设 所在直线的斜率分别为
所在直线的斜率分别为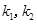 , 当
, 当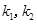 变化且满足
变化且满足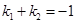 时,证明直线
时,证明直线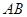 恒过定点,并求出该定点坐标.
恒过定点,并求出该定点坐标.