(本小题满分12分)已知函数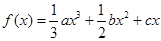
.（
）
（1）若函数
有三个零点
，且
，
，求函数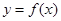 
的单调区间；
（2）若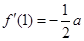
，
，试问：导函数
在区间(0，2)内是否有零点，并说明理由.
（3）在（Ⅱ）的条件下，若导函数的两个零点之间的距离不小于
，求
的取值范围.
的钢条做一个长方体容器的框架.如果所做容器的低面的一边长比另以一边长多
那么高是多少时容器的容积最大,并求出它的最大容积.
与直线
所围成图形的面积
满足
，且
为纯虚数，求证：
为实数
，观察下列不等式：
，
，…，请你猜测
将满足的不等式，并用数学归纳法加以证明。
，
。
，且函数
存在单调递减区间，求
的取值范围；
时，求函数推荐套卷
(本小题满分12分)已知函数.（）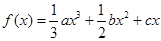
（1）若函数有三个零点，且，，求函数 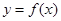的单调区间；
（2）若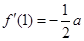，，试问：导函数在区间(0，2)内是否有零点，并说明理由.
（3）在（Ⅱ）的条件下，若导函数的两个零点之间的距离不小于，求的取值范围.
粤公网安备 44130202000953号