（本小题满分12分，（Ⅰ）小问3分，（Ⅱ）小问9分．）
直线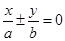
称为椭圆
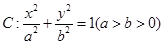的“特征直线”，若椭圆的离心率
．（1）求椭圆的“特征直线”方程；
（2）过椭圆C上一点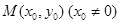
作圆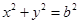
的切线，切点为P、Q，直线PQ与椭圆的“特征直线”相交于点E、F，O为坐标原点，若
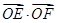取值范围恰为
，求椭圆C的方程．
。
，使
是奇函数？若存在，求出
的值；若不存在，给出证明。
时，
恒成立，求实数
且满足不等式
。
的取值范围。
。
在区间
有最小值为
，求实数
值。
，
的值；
的值。
是第二象限角，且
求
的值；
。推荐套卷
（本小题满分12分，（Ⅰ）小问3分，（Ⅱ）小问9分．）
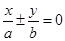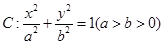直线称为椭圆的“特征直线”，若椭圆的离心率．（1）求椭圆的“特征直线”方程；
（2）过椭圆C上一点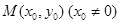作圆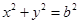的切线，切点为P、Q，直线PQ与椭圆的“特征直线”相交于点E、F，O为坐标原点，若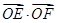取值范围恰为，求椭圆C的方程．
粤公网安备 44130202000953号