设函数
（a＞0，b，cÎR），曲线
在点P(0，f (0))处的切线方程为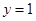
．
（Ⅰ）试确定b、c的值；
（Ⅱ）是否存在实数a使得过点（0，2）可作曲线的三条不同切线，若存在，求出a的取值范围；若不存在，请说明理由．
，
是
，
之间的一定点，并且
，
．
是直线
．且使
与直线
，求
面积的最小值．
，
，求
的值．
，试用含
的式子表示
．
，
，求证：
．
，求这个三角形的顶角的正弦、余弦及正切值．推荐套卷
设函数（a＞0，b，cÎR），曲线在点P(0，f (0))处的切线方程为．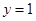
（Ⅰ）试确定b、c的值；
（Ⅱ）是否存在实数a使得过点（0，2）可作曲线的三条不同切线，若存在，求出a的取值范围；若不存在，请说明理由．
粤公网安备 44130202000953号